How Important Is Actuarial Mathematics for the Gen-Z Actuary?
Explore the core of actuarial mathematics, the foundation of precise risk calculation and management in finance and insurance, powering decisions with rigorous mathematical models and statistical analysis to optimize financial outcomes.
“We want revolutionary actuaries” was a recent statement by Tesla CEO Elon Musk. This all sounds brilliant for the tech-savvy geniuses and forward-thinking actuarial students who are planning their career around artificial intelligence, machine learning, and robotics… the revolutionary stuff, right?
Just one caveat. Before he muttered that statement, Musk noted that individuals within the actuarial profession “are great at math”. So, if you have no real interest in anything other than the cutting-edge technology, is this still a possible career for you?
WARNING: On the other hand, if you are a numeracy accomplice but a technophobe, read on at your own peril.
The Significance of Actuarial Mathematics in Modern Actuarial Practice
Actuarial Mathematics, along with ever-evolving technology, is used to develop mathematical models, allowing actuaries to quantify risks and calculate the potential significance of events given the likelihood of them occurring. Firms can then implement structures to manage the risk, either by seeking ways to mitigate a portion of it, or planning to ensure they have the means to offset the future liabilities.
This leads to fabrication of the product, be that an insurance policy, pension plan, or climate-change mitigation procedure, to name a few.
Traditionally, Actuarial Mathematics has been associated with the finance and insurance industry. Quantifying the risks allow us to arrive at suitable insurance premiums and pension policies, as well as establishing investment strategies. However, with rapidly advancing data science, actuaries can now translate their specialised mathematical knowledge into almost any avenue, be that the discovery of exoplanets, or the prevalent topic of weather risk management.

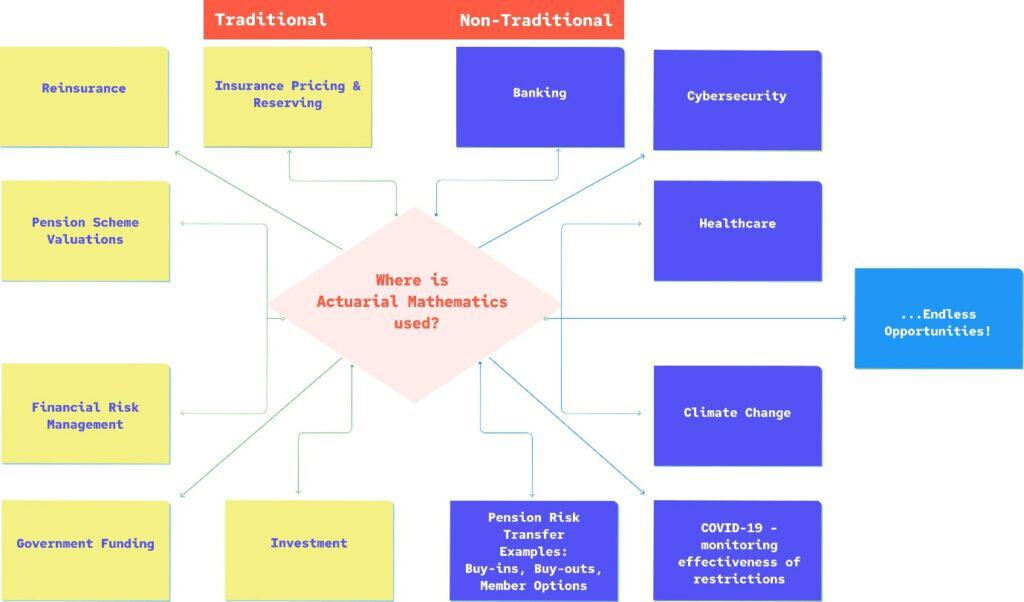
Fundamental Concepts in Actuarial Mathematics
Below is a list of the most prevalent mathematical concepts actuaries are deemed to be experts in. More examples of when these are used in the real world will be littered throughout the second half of the essay.

Probability Theory
The CORE. Actuaries can forecast the likelihood of future events with a given level of confidence. The most common probability distribution is the normal distribution – a symmetric bell-shaped curve. Binomial, Uniform, Poisson, and Geometric are common discrete distributions used, while Exponential, Gamma, and Continuous Uniform are common examples of continuous distributions. In Bayesian models, conditional probabilities can be updated as more data becomes available (the probability of event A in the future given event B has occurred).
Data Analytics / Statistical Analysis

Recognising trends in historical datasets allows actuaries to make future predictions. For example, studying the main reasons policyholders claimed on travel insurance policies within the preceding 5-year period (plus the number and severity) allows us to forecast the potential patterns over the next year. However, due to COVID-19 complications, a caveat may be to remove 2020 and 2021 travel data.
Risk Analysis
Assessing risk is a key part of all actuarial work which hinges itself on the above concepts. Calculating the probability of events, modelling the severity of each, and quantifying the total combined impact of these for the client is the basis of what many actuaries do day-to-day.
Stochastic Processes
This part is TRICKY! Traditionally this random element was used to model the trends in markets and calculate the value of financial derivatives, incorporating time, volatility, and interest rates. Examples of stochastic processes are Wiener processes, Markov chains, and Brownian motions, which model the evolution of stock prices over time.
When carefully applied, these principles may be used to model the evolution of different climate factors.
Sensitivity Analysis

Dynamic mathematical models can easily be altered to quantify the monetary impact of various independent factors to decide which conditions are worthwhile. For example, would profitability increase if an insurer deemed smokers “uninsurable”, or does the detriment of losing so many policyholders outweigh the additional risk?
Optimisation Theory
By combining various mathematical constructs, such as calculus, Markov chains and decision theory, actuaries can enable businesses to distribute resources in the most efficient and effective manner by considering how different allocations will affect profitability.
The above concepts are often interlinked and are not mutually exclusive. For example: Investment actuaries considered previous financial crises’ statistics (data analysis) to predict the likelihood (probability theory) of interest rate movements (stochastic processes) leading to a recession. Recognising the differences between crises is key; pharmaceutical companies (especially vaccine development) were impacted positively throughout COVID-19 in contrast to the 2008 mortgage crisis, therefore requiring deeper risk analysis.
The Role of Actuarial Models in Statistical Predictions
Note the importance of Mathematics in each of the models listed below which actuaries combine and use daily.
Probability, Statistical and Stochastic Models Regression Models
These assess the correlation between each explanatory variable (such as time) and the dependent variable (claim numbers). Time series models (usually show monthly, quarterly, or annual trends) can show how the month (weather) affects motorcycle claim numbers.
Generalised Linear Models

Simplistic linear regression techniques and Gaussian models cannot accurately model everything, so sometimes more complex GLMs are used with different distributions. They require three components: a probability distribution, a linear predictor, and a link function. A Normal distribution isn’t appropriate for everything, for example, a Poisson distribution is more accurate to model the force of mortality or claim frequency, while Gamma and Lognormal distributions more accurately model claim severity.
Life Contingency Models
These combine various models listed above, and model survival and death and the cash flows which begin/end based on this. They incorporate probabilities of survival, also calculated by actuaries, and the likelihood of a pay-out. This can be used to calculate premiums charged to the policyholder to ensure the insurer doesn’t make an overall loss.
Application of Actuarial Mathematics Principles in Risk Prediction
Law of Large Numbers
A formula while we’re on the topic of Mathematics:
More Data Analysed = More Reliable Results.
Solvency Requirements
European insurance companies are required to hold this annually calculated level of funds.
Time Value of Money
Remember when you could buy a Freddo bar for 10p? There’s no doubt retailers overcompensate for inflation, as a Freddo’s projected current value is around 17p (assuming a 2.33% inflation rate), rather than the hefty 25p we pay 0.10×1.023323=0.169. Over time money is worth less so goods cost more. When projecting future cash flows, for example, when considering how much money a policyholder’s contributions will be worth to them in their pension, actuaries use annuities to ensure the monetary amount of savings increases in line with inflation, so their money doesn’t deplete in value.

In the remainder of the post, I’ve provided a non-exhaustive list of routes which use many of the techniques listed above. I could type an entire blog explaining how mathematics is used in each in detail, so I hope you can see in this summary how the aforementioned translates to the industries discussed below.
Principle of Indemnity
Importance of not undercompensating claimants so the insurer profits.
Traditional Applications and Impact of Actuarial Mathematics
While many jobs are still available in traditional roles today, the industry in general seems to agree that many of these processes will eventually become automated, especially pension valuations in the first instance. From spending some time working in pensions, I would argue if a “one size fits all” approach will ever be possible for schemes. Yes, new technology is certainly automating many of the cyclical tasks, but when a new scheme arrives to be valued with its personal caveats, is a mathematical expert not vital to tailoring the initial model before it’s automated? Automation won’t happen overnight, so many Gen-Z actuaries will begin working in traditional roles.
Pensions
Modelling defined benefit schemes relies on Actuarial Mathematics to:
Model a Scheme’s Actuarial Valuations
Actuaries assess the ability of the scheme to meet its obligations (pension payments to its members). Stochastic predictions of interest and inflation rates are used to calculate the value of predicted future investment returns, ensuring these returns will cover the benefit entitlements below.
Design / Redesign a Scheme
Probability theory is used to assign the financial implications of threats to a scheme, then optimisation methods value the trade-off between investment risk vs. return to produce a viable investment strategy. The optimal asset portfolio balances risk hedging with the given scheme’s liability and investment requirements.
Calculate Benefit Entitlements

Models project an individual’s entitled benefits by combining their age, length-of-service, normal retirement age and mortality rate (benefit payments are contingent upon the member or their spouse being alive), salary (current and past), and predicted interest rates. Then using annuities, the appropriate contribution level can be calculated.
(The mortality rates themselves use data from national mortality tables, which are set by mathematically analysing census data).
Insurance
Reserving
Estimating the cost of outstanding claims and the predicted number and severity (cost) of future claims. Underestimating this leads to the insurer under-pricing, therefore having insufficient funds to pay future claims, while overestimating leads to soaring premiums and policyholders moving to a competitor. Common reserving methods: Chain Ladder and Bornhuetter-Ferguson.
Actuaries can see the impact of different events by altering their assumptions to gauge a range of reserve estimates. Their sets of assumptions could include:
- Using sensitivity analysis to exclude different people-groups.
- Altering inflation levels via stochastic processes.
- Being under and over-cautious about claim numbers and severity based on analysis of historic claims.
Pricing

Once the expected reserves are known, the premium charged to each policyholder to compensate for their risk level can be calculated. Below is a non-exhaustive list of factors to ensure the insurer’s demands are met while the policyholder is fairly charged.
- Which factors incorporate the most risk of loss (Probability Distributions), and how much more should premiums be to compensate for this? (Data Analysis)
- Did premiums last year cover obligations (including administration, rent and wages)? (Data Analysis & Principle of Indemnity)
- Each policyholder’s previous premium and claims (Data Analysis & Risk Analysis)
- Competitors’ rates (Risk Analysis)
- Allow for inflation (Time Value of Money)
Government Funding
Within healthcare, GLMs can aid the UK government in forecasting the future financial obligation to fund the NHS, impacting all taxpayers. This is just one example.
Risk Management
Remember, Risk = Reward.

Not all risk is negative. Often, actuarial work goes hand-in-hand with risk management (such as setting appropriate premiums to manage an insurer’s risk of insolvency). This can be seen many times even in this blog (even in relation to data science), but here are a few more examples:
- Reinsurance – transferring risk from one insurer to another. Risk analysis techniques are used to quantify which arrangement offloads a fitting level of risk.
- Assessing the trade-off between a client’s risk aversion level and profitability goals given their financial status. Diversifying their portfolio and developing investment strategies accordingly using optimisation theory.
- In upcoming insurance fields, such as for drones and autonomous vehicles, large volumes of data aren’t available. Models from the traditional car insurance industry can therefore be altered, incorporating the individual risks associated with each. For example, autonomous vehicles are expected to remove 90% of accident fatalities, however using the little data available to predict the probability of their systems being hacked (data analysis) allows actuaries to model the outcomes of these hacks, such as data breaches and collisions (which could also lead to fatalities). The financial impact to insurance industries from these new claim risks can be forecasted (using GLMs).
Actuarial Mathematics and Data Science: Increasing Reliability in Data Analysis
Before we talk about non-traditional routes, it’s important to mention data science, which massively impacts where we can take our skills.
Do they intersect?
Yes.
Many actuaries today are taking up positions as data scientists, but have the roles always been similar?
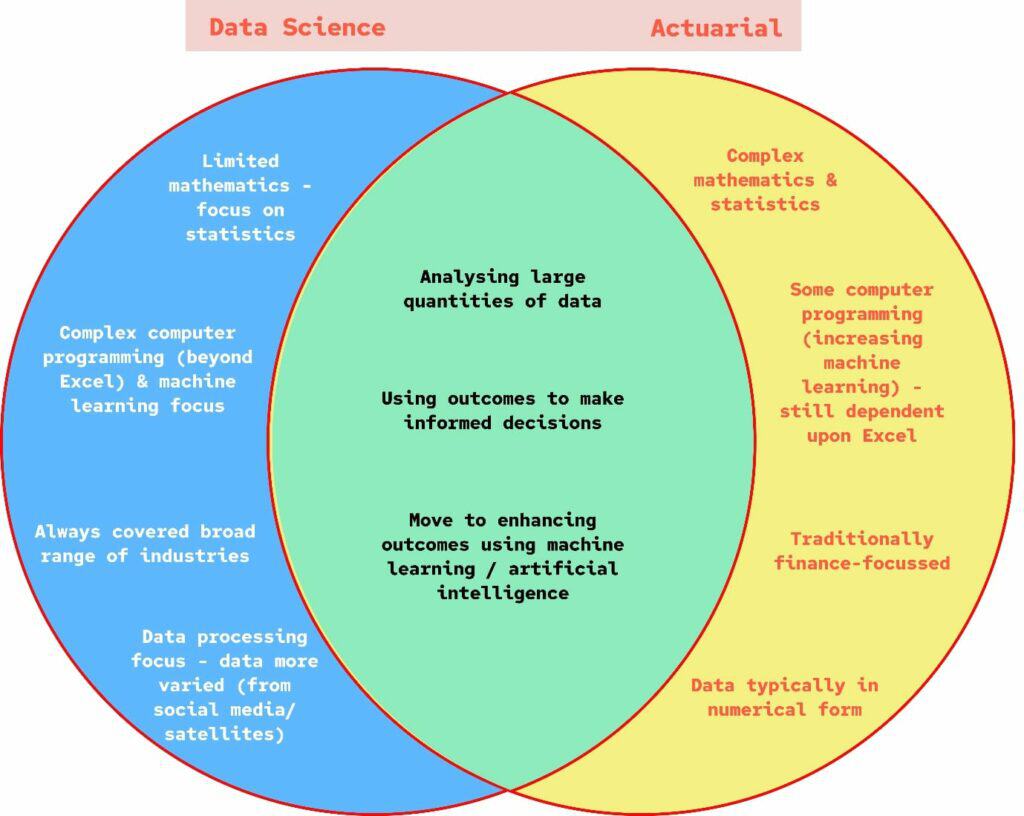
Can I just focus on one?
With the threat of many traditional actuarial roles becoming automated, non-traditional roles often rely on “big data”, which requires more computational knowledge.
Data scientists tend to be stronger at this.
However, training a machine when the principle can and cannot be used can prove more complex. All mathematical principles can’t be translated to any problem at hand, i.e. using a Geometric Brownian Motion is suitable for modelling stock prices, but it doesn’t mean we should model house prices in the same manner. Fundamental mathematical knowledge will always be fundamental for actuaries, ESPECIALLY when applying our skills to new industries.

When considering applying a current model to a new problem, we should be aware of the importance of the conditions under which the mathematics used within it can be applied, so we understand its limitations. Embarking on new territory requires us to carefully think through each step, not taking anything as given because it worked for a previous case. Eric Temple Bell wisely stated, “Obvious is the most dangerous word in mathematics”.
DISCLAIMER: I would argue that as traditional actuarial roles fade out, it is just as important to maintain a strong mathematical basis as it is to deepen our data science knowledge. This is one of the distinctive features which makes an actuary different. Gen-Z actuaries need to be mathematically competent just as much as those before them.
That being said, actuaries who build upon their data science knowledge will have a competitive edge over others. It may even be imperative for non-traditional roles.
Mathematical basis + Data Science knowledge > Mathematical basis
Application of Data Science & Actuarial Mathematics
Introducing the latest techniques can lead to major improvements in risk management, leading to optimal decision-making:
Blockchain: smart contracts are constantly building upon themselves. For example, claims on van insurance are cumulatively added to the chain (law of large numbers), which eventually will lead to automated claims processing, removing individual human judgment from the process.
Automation: periodic calculations can be automated to update to use the latest assumptions. The complex mathematical formulae don’t change, but time previously spent monotonously finding & updating assumptions before running the model can now be spent on new projects.
Visualisation: spotting trends may seem straightforward for us, but that’s not to say a graph containing millions of data points couldn’t help us recognise additional patterns. Not to mention, graphics are imperative when talking to a non-technical client. A spreadsheet won’t mean a lot to many people, but a picture (or a graph!) speaks a thousand words.

The Importance of Actuarial Mathematics in Non-Traditional Areas
Pensions Continued
Defined Contribution
The risk lies with the individual rather than the company as in defined benefit schemes. Actuaries’ financial expertise combined with their mathematical skillset can produce a model to calculate how much income an individual should invest now for retirement. It will consider:
- Time value of money
- Health of individual & life expectancy (life contingency models)
- Personal pension amount preferences
- Contribution of company
- Risk aversion (typically less risk advised with age)
Although pension valuation models can be largely automated today, current pension topics require new mathematical models, hence why AI will not replace actuaries any time soon.
GMP Rectification & Equalisation
Recent legislation means complex mathematics are required to adjust individuals’ pensions to eradicate the effects of unequal male and female GMPs over time (time value of money).
Risk Transfer
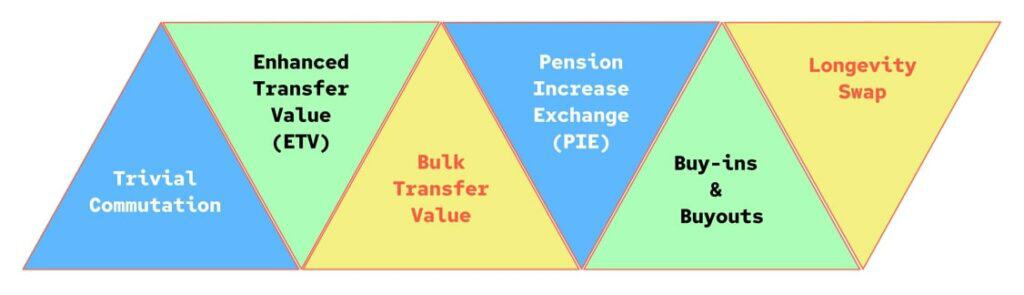
While the above member options all require mathematical models, buy-ins & buyouts are a major current topic involving an insurance company acquiring the responsibility for some (or all) of the DB scheme’s uncertainty/liabilities. Additional calculations are required on top of the valuation for the fee incurred by the scheme (based on size, life-expectancy of members, and the expected investment returns).
Financial Services & Banking

This is a new area of specialism within the IFoA qualifications. The SP10 and SA10 exams aim to equip students to understand the banking business and learn to apply mathematical methods to a banking company, affording them the opportunity to one-day hold a senior management position.
Who said actuaries had to work in the financial industry?
While deemed as financial experts, actuaries’ statistical proficiency can be used in many other fields.
By branching into cybersecurity, we can build probability models to predict the likelihood of an attack given past events, and both the financial and reputational impact this could have on their respective client, so appropriate measures can be taken.

Pricing healthcare insurance is now enhanced by big data from wearables. Watches which can gather data (heart rate, blood glucose levels etc) for individuals could lead to altered premiums. Also, while actuaries aren’t medical experts, modelling different ingredient combinations and trial outcomes, and applying optimisation techniques aids in drug development (optimal efficacy at the lowest cost). Furthermore, the UK government recognises the role of actuaries in using statistics to estimate clinical negligence claims.
While some of these COVID-19 roles may not be directly relatable to upcoming Gen-Z actuaries, they highlight the transferrable nature of our mathematical skillset.
- Probability theory helped predict death numbers based on the previous data.
- Contraction mitigation techniques (such as face-coverings) were initially mandatory in many countries, but when the infection rate fell below a calculated threshold, these measures became optional as factors such as the declination of mental health posed an increasing risk to the wellbeing of society, not to mention the economic impact. Regression models and sensitivity analysis played a vital role in balancing these trade-offs.
- Moreover, modelling the financial impact of furlough on a government and balancing this with the forecasted economic impact in the coming years, as well as the immediate monetary impact on homes throughout the region, naturally became very complex, requiring risk analysis, regression models and GLMs, with little past data to base these unprecedented decisions on.

Believe it or not, actuaries have also been known to transfer their skillset to assist in the discovery of new planets. While not necessarily actuarial, data science techniques can help to plot periods of lower light intensities from other stars reaching earth over a period indicates that something is blocking the light – an exoplanet.
Due to the huge number of already-discovered planets providing periods of lower intensity, in-depth knowledge into which period corresponds to each is required to detect additional periods. Complex data analysis can then be used to identify unknown planets’ orbit times & size based on the time and magnitude of the lower intensity.
In addition, the IFoA have now introduced a climate risk course, given scientists’ warnings concerning our planet. These impacts could affect health, having a direct impact on life insurance and pensions. Managers now opting to invest in sustainable companies could also have an impact on global investments. To this end, even traditional actuaries will need to consider how this will impact their models.

More non-traditionally, GLMs can help to model the severity of rising sea levels in a region, giving towns an idea of how much time they have to rebuild the affected infrastructure elsewhere. In motor vehicle, marine and drone insurance, models analysing risk can incorporate the increased frequency of flooding and strong winds to assess this impact on collisions, therefore claims.
There’s only so much I can say in one post, but the possibilities are ENDLESS.
Understanding and Developing Communication for Non-Actuarial Audience

Very briefly, President of the IFoA, Matt Saker, recently agreed “technical skills alone are no longer sufficient”. They say that to prove one understands mathematics, they’ll be able to explain their methods to a non-technical audience. If any prospective student intends to take the consulting route, mathematics is imperative, but clear communication skills are also key.
Concluding Insights: Key Insights and Practical Applications
“Jack of all trades, master of ONE” is not an option. While a strong basis in Actuarial Mathematics is STILL (arguably the most) essential skill for anyone seeking a career in the profession, long gone are the days of hand-written calculations (keep the battered calculator you’ve had since your GCSEs for the sentimental value though)! However, to refrain from being left behind, many would argue that we need to steer some learning time towards data science techniques. This will only add to our flare and expertise.


Having a creative mind as to where we can take our mathematical skills can help us expand our horizons, and while many current roles may become automated, we have only scratched the surface for the possibilities of actuarial mathematics’ applications!
Mathematics is our basis. Before we become technology experts. Before we communicate results. Mathematics will always be our basis.




